RPACT Multi-Arm Designs

Gernot Wassmer and Friedrich Pahlke

November 19, 2024

RPACT Multi-Arm Designs

Theoretical Background of Adaptive Designs

Clue of Combination Testing Principle (Bauer, 1989)

  • Do not pool the data of the stages, combine the stage-wise \(p\,\)-values.
  • Then the distribution of the combination function under the null does not depend on design modifications, and the adaptive test is still a test at the level \(\alpha\) for the modified design.
  • In the two stages, even different hypotheses \(H_{01}\) and \(H_{02}\) can be considered, the considered global test is a test for \(H_0 = H_{01} \cap H_{02}\).
  • Or there are multiple hypotheses at the beginning of the trials and maybe some selected.
  • Or there will be even hypotheses to be added at an interim stage (not of practical concern).
  • The rules for adapting the design need not be prespecified!

Possible Data Dependent Changes of Design

Examples of data dependent changes of design are

  • Sample size recalculation
  • Change of allocation ratio
  • Change of test statistic
  • Flexible number of looks
  • Treatment arm selection (seamless phase II/III)
  • Population selection (population enrichment)
  • Selection of endpoints

For the latter three, in general, multiple hypotheses testing applies and a closed testing procedure can be used in order to control the experimentwise error rate in a strong sense.

Methods for Multi-Arm Multi-Stage (MAMS) Designs

  • Flexible Multi-Stage Closed Combination Tests

    (Bauer & Kieser 1999; Hommel 2001, …)

    • Do not require a predefined treatment and sample size selection rule.

    • Combine two methodology concepts:

      Combination Tests and Closed Testing Principle.

  • Methods for predefined selection rules

    (Stallard & Todd 2003, Maggirr et al, 2012, …)

Closed Testing Principle, 3 Hypotheses, select one

Combination tests to be performed for the closed system of hypotheses (\(G = 3\)) for testing hypothesis \(H_0^3\) if treatment arm 3 is selected for the second stage

Closed Testing Principle, 3 Hypotheses, select two

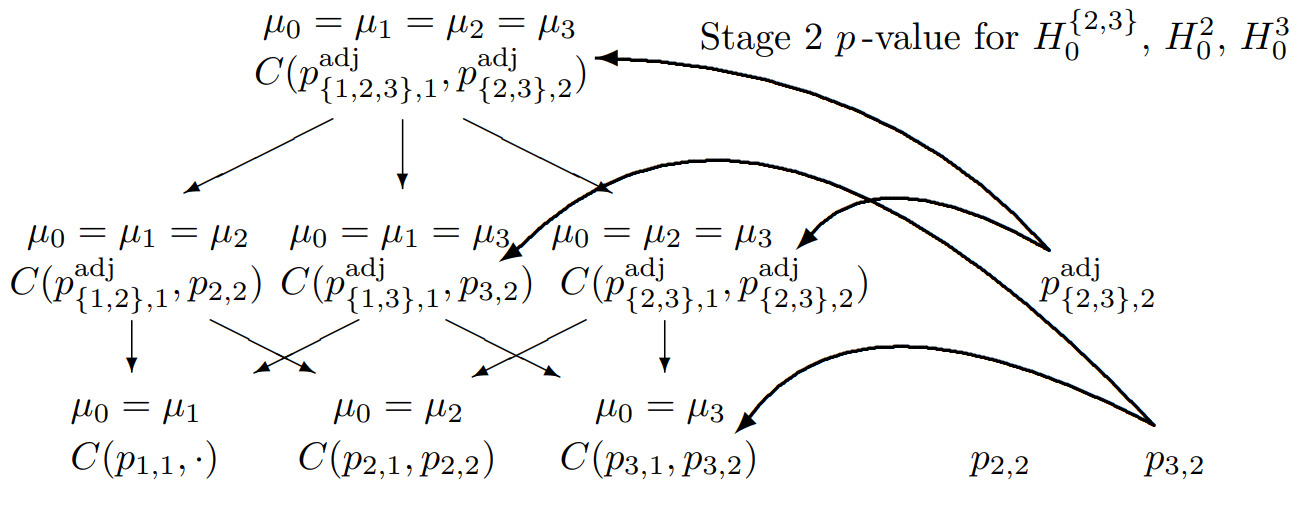
Combination tests to be performed for the closed system of hypotheses (\(G = 3\)) for testing hypothesis \(H_0^3\) if treatment arms 2 and 3 are selected for the second stage

Adaptive Designs with Treatment Arm Selection

  • Can be applied to selection of one or more than one treatment arm. The number of selected arms and the way of how to select treatment arms needs not to be preplanned.
  • Choice of combination test is free.
  • Data-driven recalculation of sample size is possible.
  • Choice of intersection tests is free. You can choose between Dunnett, Bonferroni, Simes, Sidak, hierarchical testing, etc.
  • For two-stage designs, the CRP principle can be applied: adaptive Dunnett test (König et al, 2008, Wassmer & Brannath, 2016, Section 11.1.5).
  • Confidence intervals based on stepwise testing are difficult to construct. This is a specific feature of multiple testing procedures and not of adaptive testing. Posch et al. (2005) proposed to construct repeated confidence intervals based on the single step adjusted overall p-values.

rpact Multi-Arm Analysis

Current Methods

  • Consider many-to-one comparisons comparing G active treatment arms to control.

  • Given a design and a dataset, at given stage the function

    getAnalysisResults(design, dataInput, ...)

    calculates the results of the closed test procedure, overall p-values and test statistics, conditional rejection probability (CRP), conditional power, repeated confidence intervals (RCIs), and repeated overall p-values.

  • design is either from getDesignInverseNormal() or getDesignFisher() (or NULL)

  • For two stages, design <- getDesignConditionalDunnett() can be selected.

Multi-Arm Analysis

  • The conditional power is calculated only if (at least) the sample size nPlanned for the subsequent stage(s) is specified.
  • dataInput is the summary data used for calculating the test results. This is either an element of DataSetMeans, of DataSetRates, or of DataSetSurvival.
  • dataInput is defined through getDataset(), rpact identifies the type of endpoint.
  • In rpact 3.0, getDataset() is generalized to an arbitrary number of treatment arms.

Multi-Arm Analysis

dataInput

  • An element of DataSetMeans for one sample is created by

    getDataset(means =, stDevs =, sampleSizes =)

    where means, stDevs, sampleSizes are vectors with stagewise means, standard deviations, and sample sizes of length given by the number of available stages.

  • An element of DataSetMeans for two samples is created by

    getDataset(means1 =, means2 =, stDevs1 =, stDevs2 =, sampleSizes1 =, sampleSizes2 =)

    where means1, means2, stDevs1, stDevs2, sampleSizes1, sampleSizes2 are vectors with stagewise means, standard deviations, and sample sizes for the two treatment groups of length given by the number of available stages.

Multi-Arm Analysis

dataInput

  • An element of DataSetMeans for G + 1 samples is created by

    getDataset(means1 =,..., means[G+1] =, stDevs1 =, ..., stDevs[G+1] =, sampleSizes1 =, ..., sampleSizes[G+1] =),

    where means1, ..., means[G+1], stDevs1, ..., stDevs[G+1], sampleSizes1, ..., sampleSizes[G+1] are vectors with stagewise means, standard deviations, and sample sizes for G+1 treatment groups of length given by the number of available stages.

  • Last treatment arm G + 1 always refers to the control group that cannot be deselected.

  • Only for the first stage all treatment arms needs to be specified, so treatment arm selection with an arbitrary number of treatment arms for subsequent stage can be considered.

  • Analogue definition of DataSetRates and DataSetSurvival.

Multi-Arm Analysis Example

exampleMeans <- getDataset(
    n1      = c( 23,  25),
    n2      = c( 25,  NA),
    n3      = c( 24,  27),
    n4      = c( 22,  29),
    means1  = c(2.41, 2.27),
    means2  = c(1.38,  NA),
    means3  = c(2.07, 2.01),
    means4  = c(0.92, 1.02),
    stDevs1 = c(2.24, 2.21),
    stDevs2 = c(2.12,  NA),
    stDevs3 = c(2.56, 2.32),
    stDevs4 = c(2.15, 2.21)
)

Multi-Arm Analysis Example

designIN <- getDesignInverseNormal(
  typeOfDesign = "WT",
  deltaWT = 0.25, 
  informationRates = c(0.25, 0.5, 1)
)
results <- designIN |> 
    getAnalysisResults(dataInput = exampleMeans)
results |> print()

Multi-arm analysis results (means of 4 groups, inverse normal combination test design)

Design parameters

  • Fixed weights: 0.500, 0.500, 0.707
  • Critical values: 2.904, 2.442, 2.053
  • Futility bounds (non-binding): -Inf, -Inf
  • Cumulative alpha spending: 0.001843, 0.008414, 0.025000
  • Local one-sided significance levels: 0.001843, 0.007307, 0.020021
  • Significance level: 0.0250
  • Test: one-sided

Default parameters

  • Normal approximation: FALSE
  • Direction upper: TRUE
  • Theta H0: 0
  • Intersection test: Dunnett
  • Variance option: overallPooled

Stage results

  • Cumulative effect sizes (1): 1.490, 1.360, NA
  • Cumulative effect sizes (2): 0.460, NA, NA
  • Cumulative effect sizes (3): 1.150, 1.061, NA
  • Cumulative (pooled) standard deviations (1): 2.197, 2.182, NA
  • Cumulative (pooled) standard deviations (2): 2.134, NA, NA
  • Cumulative (pooled) standard deviations (3): 2.373, 2.291, NA
  • Stage-wise test statistics (1): 2.196, 2.038, NA
  • Stage-wise test statistics (2): 0.691, NA, NA
  • Stage-wise test statistics (3): 1.712, 1.647, NA
  • Separate p-values (1): 0.01535, 0.02246, NA
  • Separate p-values (2): 0.24552, NA, NA
  • Separate p-values (3): 0.04516, 0.05176, NA

Adjusted stage-wise p-values

  • Treatments 1, 2, 3 vs. control: 0.03904, 0.04112, NA
  • Treatments 1, 2 vs. control: 0.02806, 0.02246, NA
  • Treatments 1, 3 vs. control: 0.02810, 0.04112, NA
  • Treatments 2, 3 vs. control: 0.07879, 0.05176, NA
  • Treatment 1 vs. control: 0.01535, 0.02246, NA
  • Treatment 2 vs. control: 0.24552, NA, NA
  • Treatment 3 vs. control: 0.04516, 0.05176, NA

Overall adjusted test statistics

  • Treatments 1, 2, 3 vs. control: 1.762, 2.475, NA
  • Treatments 1, 2 vs. control: 1.910, 2.769, NA
  • Treatments 1, 3 vs. control: 1.909, 2.579, NA
  • Treatments 2, 3 vs. control: 1.413, 2.151, NA
  • Treatment 1 vs. control: 2.161, 2.946, NA
  • Treatment 2 vs. control: 0.689, NA, NA
  • Treatment 3 vs. control: 1.694, 2.349, NA

Test actions

  • Rejected (1): FALSE, TRUE, NA
  • Rejected (2): FALSE, FALSE, NA
  • Rejected (3): FALSE, FALSE, NA

Further analysis results

  • Conditional rejection probability (1): 0.11367, 0.33392, NA
  • Conditional rejection probability (2): 0.02593, NA, NA
  • Conditional rejection probability (3): 0.07194, 0.22563, NA
  • Conditional power (1): NA, NA, NA
  • Conditional power (2): NA, NA, NA
  • Conditional power (3): NA, NA, NA
  • Confidence intervals (lower) (1): -0.76273, 0.01443, NA
  • Confidence intervals (lower) (2): -1.74824, NA, NA
  • Confidence intervals (lower) (3): -1.07967, -0.26374, NA
  • Confidence intervals (upper) (1): 3.743, 2.719, NA
  • Confidence intervals (upper) (2): 2.668, NA, NA
  • Confidence intervals (upper) (3): 3.380, 2.399, NA
  • Overall p-values (1): 0.15176, 0.02326, NA
  • Overall p-values (2): 0.46577, NA, NA
  • Overall p-values (3): 0.23285, 0.04597, NA

Legend

  • (i): results of treatment arm i vs. control group 4

Multi-Arm Analysis Example

results |> summary()

Multi-arm analysis results for a continuous endpoint (3 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm t-test, Dunnett intersection test, overall pooled variances option. H0: mu(i) - mu(control) = 0 against H1: mu(i) - mu(control) > 0.

Stage 1 2 3
Fixed weight 0.5 0.5 0.707
Cumulative alpha spent 0.0018 0.0084 0.0250
Stage levels (one-sided) 0.0018 0.0073 0.0200
Efficacy boundary (z-value scale) 2.904 2.442 2.053
Cumulative effect size (1) 1.490 1.360
Cumulative effect size (2) 0.460
Cumulative effect size (3) 1.150 1.061
Cumulative (pooled) standard deviation 2.276 2.263
Stage-wise test statistic (1) 2.196 2.038
Stage-wise test statistic (2) 0.691
Stage-wise test statistic (3) 1.712 1.647
Stage-wise p-value (1) 0.0153 0.0225
Stage-wise p-value (2) 0.2455
Stage-wise p-value (3) 0.0452 0.0518
Adjusted stage-wise p-value (1, 2, 3) 0.0390 0.0411
Adjusted stage-wise p-value (1, 2) 0.0281 0.0225
Adjusted stage-wise p-value (1, 3) 0.0281 0.0411
Adjusted stage-wise p-value (2, 3) 0.0788 0.0518
Adjusted stage-wise p-value (1) 0.0153 0.0225
Adjusted stage-wise p-value (2) 0.2455
Adjusted stage-wise p-value (3) 0.0452 0.0518
Overall adjusted test statistic (1, 2, 3) 1.762 2.475
Overall adjusted test statistic (1, 2) 1.910 2.769
Overall adjusted test statistic (1, 3) 1.909 2.579
Overall adjusted test statistic (2, 3) 1.413 2.151
Overall adjusted test statistic (1) 2.161 2.946
Overall adjusted test statistic (2) 0.689
Overall adjusted test statistic (3) 1.694 2.349
Test action: reject (1) FALSE TRUE
Test action: reject (2) FALSE FALSE
Test action: reject (3) FALSE FALSE
Conditional rejection probability (1) 0.1137 0.3339
Conditional rejection probability (2) 0.0259
Conditional rejection probability (3) 0.0719 0.2256
95% repeated confidence interval (1) [-0.763; 3.743] [0.014; 2.719]
95% repeated confidence interval (2) [-1.748; 2.668]
95% repeated confidence interval (3) [-1.080; 3.380] [-0.264; 2.399]
Repeated p-value (1) 0.1518 0.0233
Repeated p-value (2) 0.4658
Repeated p-value (3) 0.2329 0.0460

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

Multi-Arm Analysis Example

results |> plot(, type = 2)

Multi-Arm Analysis Example

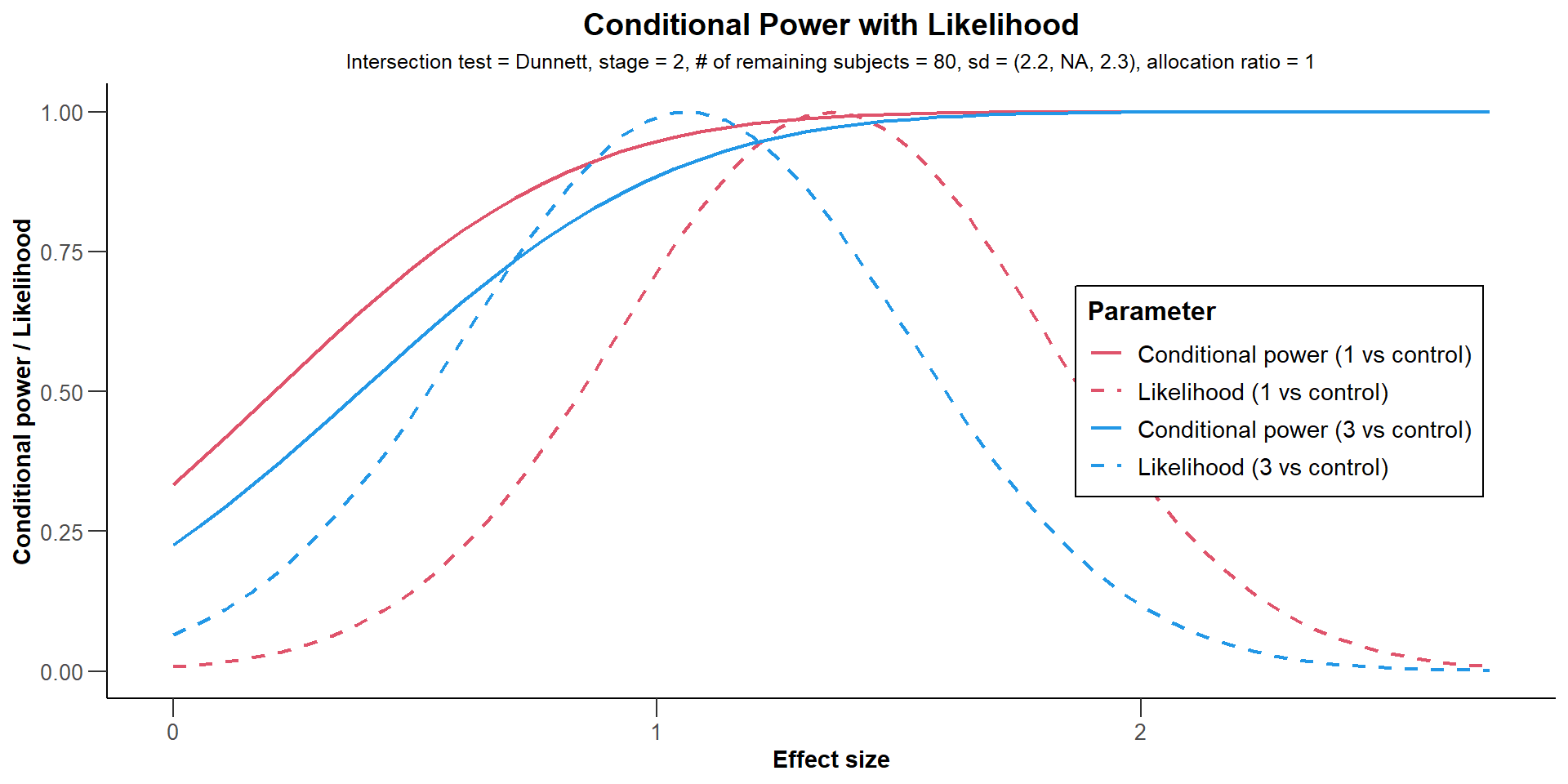
Conditional Power

result <- designIN |> 
    getAnalysisResults(
        dataInput = exampleMeans, 
        nPlanned = 80
    )
result |> summary()

Multi-arm analysis results for a continuous endpoint (3 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm t-test, Dunnett intersection test, overall pooled variances option. H0: mu(i) - mu(control) = 0 against H1: mu(i) - mu(control) > 0. The conditional power calculation with planned sample size is based on overall effect: thetaH1(1) = 1.36, thetaH1(2) = NA, thetaH1(3) = 1.06 and overall standard deviation: sd(1) = 2.18, sd(2) = NA, sd(3) = 2.29.

Stage 1 2 3
Fixed weight 0.5 0.5 0.707
Cumulative alpha spent 0.0018 0.0084 0.0250
Stage levels (one-sided) 0.0018 0.0073 0.0200
Efficacy boundary (z-value scale) 2.904 2.442 2.053
Cumulative effect size (1) 1.490 1.360
Cumulative effect size (2) 0.460
Cumulative effect size (3) 1.150 1.061
Cumulative (pooled) standard deviation 2.276 2.263
Stage-wise test statistic (1) 2.196 2.038
Stage-wise test statistic (2) 0.691
Stage-wise test statistic (3) 1.712 1.647
Stage-wise p-value (1) 0.0153 0.0225
Stage-wise p-value (2) 0.2455
Stage-wise p-value (3) 0.0452 0.0518
Adjusted stage-wise p-value (1, 2, 3) 0.0390 0.0411
Adjusted stage-wise p-value (1, 2) 0.0281 0.0225
Adjusted stage-wise p-value (1, 3) 0.0281 0.0411
Adjusted stage-wise p-value (2, 3) 0.0788 0.0518
Adjusted stage-wise p-value (1) 0.0153 0.0225
Adjusted stage-wise p-value (2) 0.2455
Adjusted stage-wise p-value (3) 0.0452 0.0518
Overall adjusted test statistic (1, 2, 3) 1.762 2.475
Overall adjusted test statistic (1, 2) 1.910 2.769
Overall adjusted test statistic (1, 3) 1.909 2.579
Overall adjusted test statistic (2, 3) 1.413 2.151
Overall adjusted test statistic (1) 2.161 2.946
Overall adjusted test statistic (2) 0.689
Overall adjusted test statistic (3) 1.694 2.349
Test action: reject (1) FALSE TRUE
Test action: reject (2) FALSE FALSE
Test action: reject (3) FALSE FALSE
Conditional rejection probability (1) 0.1137 0.3339
Conditional rejection probability (2) 0.0259
Conditional rejection probability (3) 0.0719 0.2256
Planned sample size 80
Conditional power (1) 0.9908
Conditional power (2)
Conditional power (3) 0.9064
95% repeated confidence interval (1) [-0.763; 3.743] [0.014; 2.719]
95% repeated confidence interval (2) [-1.748; 2.668]
95% repeated confidence interval (3) [-1.080; 3.380] [-0.264; 2.399]
Repeated p-value (1) 0.1518 0.0233
Repeated p-value (2) 0.4658
Repeated p-value (3) 0.2329 0.0460

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

Multi-Arm Analysis Example

Conditional Power

result |> plot(type = 1)

Multi-Arm Analysis Example

Final stage

exampleMeans <- getDataset(
    n1      = c( 23,  25, NA),
    n2      = c( 25,  NA, NA),
    n3      = c( 24,  27, 42),
    n4      = c( 22,  29, 47),
    means1  = c(2.41, 2.27, NA),
    means2  = c(1.38,  NA, NA),
    means3  = c(2.07, 2.01, 2.05),
    means4  = c(0.92, 1.02, 1.05),
    stDevs1 = c(2.24, 2.21, NA),
    stDevs2 = c(2.12,  NA, NA),
    stDevs3 = c(2.56, 2.32, 2.15),
    stDevs4 = c(2.15, 2.21, 2.09)
)

designIN |> getAnalysisResults(
  dataInput = exampleMeans
) |> summary()

Multi-arm analysis results for a continuous endpoint (3 active arms vs. control)

Sequential analysis with 3 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a multi-arm t-test, Dunnett intersection test, overall pooled variances option. H0: mu(i) - mu(control) = 0 against H1: mu(i) - mu(control) > 0.

Stage 1 2 3
Fixed weight 0.5 0.5 0.707
Cumulative alpha spent 0.0018 0.0084 0.0250
Stage levels (one-sided) 0.0018 0.0073 0.0200
Efficacy boundary (z-value scale) 2.904 2.442 2.053
Cumulative effect size (1) 1.490 1.360
Cumulative effect size (2) 0.460
Cumulative effect size (3) 1.150 1.061 1.032
Cumulative (pooled) standard deviation 2.276 2.263 2.201
Stage-wise test statistic (1) 2.196 2.038
Stage-wise test statistic (2) 0.691
Stage-wise test statistic (3) 1.712 1.647 2.223
Stage-wise p-value (1) 0.0153 0.0225
Stage-wise p-value (2) 0.2455
Stage-wise p-value (3) 0.0452 0.0518 0.0144
Adjusted stage-wise p-value (1, 2, 3) 0.0390 0.0411 0.0144
Adjusted stage-wise p-value (1, 2) 0.0281 0.0225
Adjusted stage-wise p-value (1, 3) 0.0281 0.0411 0.0144
Adjusted stage-wise p-value (2, 3) 0.0788 0.0518 0.0144
Adjusted stage-wise p-value (1) 0.0153 0.0225
Adjusted stage-wise p-value (2) 0.2455
Adjusted stage-wise p-value (3) 0.0452 0.0518 0.0144
Overall adjusted test statistic (1, 2, 3) 1.762 2.475 3.296
Overall adjusted test statistic (1, 2) 1.910 2.769
Overall adjusted test statistic (1, 3) 1.909 2.579 3.369
Overall adjusted test statistic (2, 3) 1.413 2.151 3.066
Overall adjusted test statistic (1) 2.161 2.946
Overall adjusted test statistic (2) 0.689
Overall adjusted test statistic (3) 1.694 2.349 3.207
Test action: reject (1) FALSE TRUE TRUE
Test action: reject (2) FALSE FALSE FALSE
Test action: reject (3) FALSE FALSE TRUE
Conditional rejection probability (1) 0.1137 0.3339
Conditional rejection probability (2) 0.0259
Conditional rejection probability (3) 0.0719 0.2256
95% repeated confidence interval (1) [-0.763; 3.743] [0.014; 2.719]
95% repeated confidence interval (2) [-1.748; 2.668]
95% repeated confidence interval (3) [-1.080; 3.380] [-0.264; 2.399] [0.244; 1.827]
Repeated p-value (1) 0.1518 0.0233
Repeated p-value (2) 0.4658
Repeated p-value (3) 0.2329 0.0460 0.0012

Legend:

  • (i): results of treatment arm i vs. control arm
  • (i, j, …): comparison of treatment arms ‘i, j, …’ vs. control arm

rpact Multi-Arm Simulation

Overview

getSimulationMultiArmMeans(design,...),

getSimulationMultiArmRates(design,...), and

getSimulationMultiArmSurvival(design,...)

  • perform simulations in multi-arm designs for testing means, rates, and hazard ratios, respectively.

  • You can assess different treatment arm selection strategies, sample size reassessment methods, general stopping, and stopping for futility rules.

  • Define selection strategy and effect size pattern appropriately (e.g., linear, sigmoidEmax, user defined, etc).

  • New parameter doseLevels will be available for next CRAN release (already on gitHub)

Time to Event example:

  • Time to disease progression event

  • 2 active arms, 1 control arm

  • Equal allocation between groups

  • Power 90%

  • \(\alpha\) = 0.025 one sided

  • 2 analyses (1 IA at 50% events) futility analysis at interim and select best dose based on highest HR

  • Assume median TTE in control arm: 25 months

  • Median TTE in active: 18 months so target HR 0.72

  • Accrual: Assume 10 for first 10 months, then 20 for next 10 then 30 per month thereafter for max 36 months (or feel free to use a constant accrual rate)

Sample Size Calculation

Around 390 events are needed to achieve 90% power for a two-sample comparison:

getSampleSizeSurvival(
    alpha = 0.025,
    beta = 0.1,
    median2 = 25,
    hazardRatio = 0.72,
    accrualTime = c(0, 10, 20, 36),
    accrualIntensity = c(10, 20, 30)
) |> summary()

Sample size calculation for a survival endpoint

Fixed sample analysis, one-sided significance level 2.5%, power 90%. The results were calculated for a two-sample logrank test, H0: hazard ratio = 1, H1: hazard ratio = 0.72, control median(2) = 25, accrual time = c(10, 20, 36), accrual intensity = c(10, 20, 30).

Stage Fixed
Stage level (one-sided) 0.0250
Efficacy boundary (z-value scale) 1.960
Efficacy boundary (t) 0.820
Number of subjects 780.0
Number of events 389.5
Analysis time 52.02
Expected study duration under H1 52.02

Legend:

  • (t): treatment effect scale

Design with Interim Stage and Bonferroni

getDesignInverseNormal(
    kMax = 2,
    typeOfDesign = "noEarlyEfficacy",
    alpha = 0.0125,
    beta = 0.1,
    futilityBounds = 0
) |> getSampleSizeSurvival(
    median2 = 25,
    hazardRatio = 0.72,
    accrualTime = c(0, 10, 20, 36),
    accrualIntensity = c(10, 20, 30)
) |> summary()

Sample size calculation for a survival endpoint

Sequential analysis with a maximum of 2 looks (inverse normal combination test design), one-sided overall significance level 1.25%, power 90%. The results were calculated for a two-sample logrank test, H0: hazard ratio = 1, H1: hazard ratio = 0.72, control median(2) = 25, accrual time = c(10, 20, 36), accrual intensity = c(10, 20, 30).

Stage 1 2
Fixed weight 0.707 0.707
Cumulative alpha spent 0 0.0125
Stage levels (one-sided) 0 0.0125
Efficacy boundary (z-value scale) Inf 2.241
Futility boundary (z-value scale) 0
Efficacy boundary (t) 0 0.812
Futility boundary (t) 1.000
Cumulative power 0 0.9000
Number of subjects 780.0 780.0
Expected number of subjects under H1 780.0
Cumulative number of events 230.8 461.6
Expected number of events under H1 460.2
Analysis time 37.53 60.77
Expected study duration under H1 60.62
Overall exit probability (under H0) 0.5000
Overall exit probability (under H1) 0.0063
Exit probability for efficacy (under H0) 0
Exit probability for efficacy (under H1) 0
Exit probability for futility (under H0) 0.5000
Exit probability for futility (under H1) 0.0063

Legend:

  • (t): treatment effect scale

A Multi-Arm Approach

  • Based on this result, we plan a multi-arm design with a maximum of 460 events in order to achieve power 90%

  • The procedure is designed in such a way that in case of selecting a treatment arm the specified events need to be observed for the remaining arms (i.e., no event number recalculation)

  • Note, for multi-armed designs, to simulate TTE on a patient level is not available. However, in rpact the approach of Deng et al (2019) for simulating normally distributed log-rank statistics is implemented

  • The number of events for pairwise comparisons are estimated from the assumption about the hazard ratios

  • This provides a reasonable approximation for the assessment of test characteristics, i.e., for the estimation of power and selection probabilities.

Example Select All

design <- getDesignInverseNormal(
    kMax = 2,
    typeOfDesign = "noEarlyEfficacy",
    alpha = 0.025,
    futilityBounds = 0
)
effectMatrix = matrix(
    c(0.72, 0.72,
    0.72, 0.8,
    0.72, 0.9,
    0.8, 0.8,
    0.8, 0.9,
    1, 1), 
    ncol = 2, byrow = TRUE
)
design |> getSimulationMultiArmSurvival(
    activeArms = 2,
    directionUpper = FALSE,
    typeOfShape = "userDefined",
    effectMatrix = effectMatrix,
    typeOfSelection = "all",
    plannedEvents = c(230, 460),
    maxNumberOfIterations = 1000,
    seed = 123
) |> print()

Example Select All

Simulation of multi-arm survival data (inverse normal combination test design):

Design parameters:
  Information rates                      : 0.500, 1.000 
  Critical values                        : Inf, 1.960 
  Futility bounds (non-binding)          : 0.000 
  Cumulative alpha spending              : 0.0000, 0.0250 
  Local one-sided significance levels    : 0.0000, 0.0250 
  Significance level                     : 0.0250 
  Test                                   : one-sided 

User defined parameters:
  Seed                                   : 123 
  Direction upper                        : FALSE 
  Planned cumulative events              : 230, 460 
  Active arms                            : 2 
  Effect matrix (1)                      : 0.72, 0.72, 0.72, 0.80, 0.80, 1.00 
  Effect matrix (2)                      : 0.72, 0.80, 0.90, 0.80, 0.90, 1.00 
  Type of shape                          : userDefined 
  Type of selection                      : all 

Derived from user defined parameters:
  omega_max                              : 0.720, 0.800, 0.900, 0.800, 0.900, 1.000 

Default parameters:
  Maximum number of iterations           : 1000 
  Planned allocation ratio               : 1 
  Calculate events function              : default 
  Slope                                  : 1 
  Intersection test                      : Dunnett 
  Adaptations                            : TRUE 
  Effect measure                         : effectEstimate 
  Success criterion                      : all 
  Epsilon value                          : NA 
  r value                                : NA 
  Threshold                              : -Inf 

Results:
  Cumulative number of events (1) [1]    : 162.1, 157, 151, 159.2, 153.3, 153.3 
  Cumulative number of events (1) [2]    : 324.3, 314, 302, 318.5, 306.7, 306.7 
  Cumulative number of events (2) [1]    : 162.1, 164.3, 166.8, 159.2, 161.9, 153.3 
  Cumulative number of events (2) [2]    : 324.3, 328.6, 333.6, 318.5, 323.7, 306.7 
  Iterations [1]                         : 1000, 1000, 1000, 1000, 1000, 1000 
  Iterations [2]                         : 994, 983, 956, 937, 876, 503 
  Reject at least one                    : 0.9080, 0.8020, 0.6990, 0.5770, 0.3670, 0.0190 
  Rejected arms per stage (1) [1]        : 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000 
  Rejected arms per stage (1) [2]        : 0.8290, 0.7630, 0.6930, 0.4490, 0.3510, 0.0150 
  Rejected arms per stage (2) [1]        : 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000 
  Rejected arms per stage (2) [2]        : 0.8240, 0.4990, 0.1530, 0.4580, 0.1170, 0.0110 
  Futility stop per stage                : 0.0060, 0.0170, 0.0440, 0.0630, 0.1240, 0.4970 
  Early stop                             : 0.0060, 0.0170, 0.0440, 0.0630, 0.1240, 0.4970 
  Success per stage [1]                  : 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000 
  Success per stage [2]                  : 0.7450, 0.4600, 0.1470, 0.3300, 0.1010, 0.0070 
  Selected arms (1) [1]                  : 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000 
  Selected arms (1) [2]                  : 0.9940, 0.9830, 0.9560, 0.9370, 0.8760, 0.5030 
  Selected arms (2) [1]                  : 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000 
  Selected arms (2) [2]                  : 0.9940, 0.9830, 0.9560, 0.9370, 0.8760, 0.5030 
  Number of active arms [1]              : 2.000, 2.000, 2.000, 2.000, 2.000, 2.000 
  Number of active arms [2]              : 2.000, 2.000, 2.000, 2.000, 2.000, 2.000 
  Expected number of events              : 458.6, 456.1, 449.9, 445.5, 431.5, 345.7 
  Single number of events {1} [1]        : 67.9, 65.7, 63.2, 70.8, 68.1, 76.7 
  Single number of events {1} [2]        : 67.9, 65.7, 63.2, 70.8, 68.1, 76.7 
  Single number of events {2} [1]        : 67.9, 73, 79, 70.8, 76.7, 76.7 
  Single number of events {2} [2]        : 67.9, 73, 79, 70.8, 76.7, 76.7 
  Single number of events {control} [1]  : 94.3, 91.3, 87.8, 88.5, 85.2, 76.7 
  Single number of events {control} [2]  : 94.3, 91.3, 87.8, 88.5, 85.2, 76.7 
  Conditional power (achieved) [1]       : NA, NA, NA, NA, NA, NA 
  Conditional power (achieved) [2]       : 0.8718, 0.8029, 0.7665, 0.6935, 0.5708, 0.2924 

Legend:
  (i): values of treatment arm i compared to control
  {j}: values of treatment arm j
  [k]: values at stage k

Example Select the Best

tictoc::tic()
design |> getSimulationMultiArmSurvival(
    activeArms = 2,
    directionUpper = FALSE,
    typeOfShape = "userDefined",
    effectMatrix = effectMatrix,
    typeOfSelection = "best",
    plannedEvents = c(230, 460),
    maxNumberOfIterations = 1000,
    seed = 123
) |> print()

Example Select the Best

Simulation of multi-arm survival data (inverse normal combination test design):

Design parameters:
  Information rates                      : 0.500, 1.000 
  Critical values                        : Inf, 1.960 
  Futility bounds (non-binding)          : 0.000 
  Cumulative alpha spending              : 0.0000, 0.0250 
  Local one-sided significance levels    : 0.0000, 0.0250 
  Significance level                     : 0.0250 
  Test                                   : one-sided 

User defined parameters:
  Seed                                   : 123 
  Direction upper                        : FALSE 
  Planned cumulative events              : 230, 460 
  Active arms                            : 2 
  Effect matrix (1)                      : 0.72, 0.72, 0.72, 0.80, 0.80, 1.00 
  Effect matrix (2)                      : 0.72, 0.80, 0.90, 0.80, 0.90, 1.00 
  Type of shape                          : userDefined 

Derived from user defined parameters:
  omega_max                              : 0.720, 0.800, 0.900, 0.800, 0.900, 1.000 

Default parameters:
  Maximum number of iterations           : 1000 
  Planned allocation ratio               : 1 
  Calculate events function              : default 
  Slope                                  : 1 
  Intersection test                      : Dunnett 
  Adaptations                            : TRUE 
  Type of selection                      : best 
  Effect measure                         : effectEstimate 
  Success criterion                      : all 
  Epsilon value                          : NA 
  r value                                : NA 
  Threshold                              : -Inf 

Results:
  Cumulative number of events (1) [1]    : 162.1, 157, 151, 159.2, 153.3, 153.3 
  Cumulative number of events (1) [2]    : 340.9, 358.4, 372.5, 337.8, 360.9, 324.6 
  Cumulative number of events (2) [1]    : 162.1, 164.3, 166.8, 159.2, 161.9, 153.3 
  Cumulative number of events (2) [2]    : 347.1, 325, 308.1, 338.4, 310.7, 327.1 
  Iterations [1]                         : 1000, 1000, 1000, 1000, 1000, 1000 
  Iterations [2]                         : 990, 989, 944, 944, 897, 466 
  Reject at least one                    : 0.9210, 0.8220, 0.7930, 0.6350, 0.4900, 0.0260 
  Rejected arms per stage (1) [1]        : 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000 
  Rejected arms per stage (1) [2]        : 0.4310, 0.6400, 0.7710, 0.3200, 0.4410, 0.0130 
  Rejected arms per stage (2) [1]        : 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000 
  Rejected arms per stage (2) [2]        : 0.4900, 0.1820, 0.0220, 0.3150, 0.0490, 0.0130 
  Futility stop per stage                : 0.0100, 0.0110, 0.0560, 0.0560, 0.1030, 0.5340 
  Early stop                             : 0.0100, 0.0110, 0.0560, 0.0560, 0.1030, 0.5340 
  Success per stage [1]                  : 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000 
  Success per stage [2]                  : 0.9210, 0.8220, 0.7930, 0.6350, 0.4900, 0.0260 
  Selected arms (1) [1]                  : 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000 
  Selected arms (1) [2]                  : 0.4630, 0.7120, 0.8700, 0.4690, 0.7120, 0.2280 
  Selected arms (2) [1]                  : 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000 
  Selected arms (2) [2]                  : 0.5270, 0.2770, 0.0740, 0.4750, 0.1850, 0.2380 
  Number of active arms [1]              : 2.000, 2.000, 2.000, 2.000, 2.000, 2.000 
  Number of active arms [2]              : 1.000, 1.000, 1.000, 1.000, 1.000, 1.000 
  Expected number of events              : 457.7, 457.5, 447.1, 447.1, 436.3, 337.2 
  Single number of events {1} [1]        : 67.9, 65.7, 63.2, 70.8, 68.1, 76.7 
  Single number of events {1} [2]        : 45, 69.3, 88.7, 50.8, 81.1, 56.3 
  Single number of events {2} [1]        : 67.9, 73, 79, 70.8, 76.7, 76.7 
  Single number of events {2} [2]        : 51.3, 28.6, 8.5, 51.4, 22.5, 58.7 
  Single number of events {control} [1]  : 94.3, 91.3, 87.8, 88.5, 85.2, 76.7 
  Single number of events {control} [2]  : 133.7, 132.1, 132.7, 127.8, 126.4, 115 
  Conditional power (achieved) [1]       : NA, NA, NA, NA, NA, NA 
  Conditional power (achieved) [2]       : 0.8675, 0.7846, 0.7430, 0.6803, 0.5998, 0.3370 

Legend:
  (i): values of treatment arm i compared to control
  {j}: values of treatment arm j
  [k]: values at stage k
tictoc::toc()
3.39 sec elapsed

Summary

  • Introduction to design and analysis of multi-arm multi-stage designs with use of flexible closed combination testing principle which strongly controls the familywise Type I error rate
  • Fast simulation in getSimulationMultiArm...() for reasonable activeArms and maxNumberOfIterations
  • Through selection procedure there might be a gain in power
  • Consider different situations through specification of effectMatrix
  • Assessment of futility stops
  • Simulation for survival designs on the patient level not possible (yet)

Questions??